by Alessia Leibert
October 2022
Minnesota ranks fourth lowest in the nation for percentage of women in poverty1, and 12th highest for the percent of women with a Bachelor's degree or higher credential. Despite these accomplishments, female workers in Minnesota experience lower earnings compared to their male peers.
This study analyzes the role of math proficiency in contributing to gender pay gaps in Minnesota. Specifically, it compares female high school graduates to their male peers with the aim of identifying (1) if a gender math gap exists, (2) how the math gap influences educational choices in secondary and postsecondary school, (3) how the math gap contributes to gender wage disparities years after high school, and (4) implications of the findings.
The dataset consists of 142,909 individuals who graduated from a Minnesota public high school between June 2013 and June 2015. Since we know their high school experiences and labor market histories, we can identify the earliest points in life when gender wage gaps emerge and formulate hypotheses on how math proficiency contributes to their formation. This evidence can help to craft policy responses to address the problem.
Standardized scores in the MCA2 math test administered in eighth grade show that a bigger share of girls scored below the median than boys, 51% versus 48% (Figure 1).
Figure 1
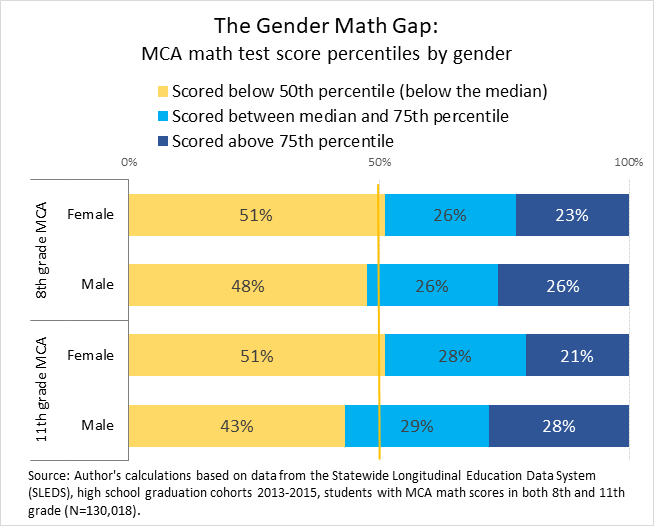
The gap in the same group of students is even larger in eleventh grade, with 51% of girls scoring below the median to 43% of boys, and 21% scoring above the seventy-fifth percentile versus 28% among boys3. This indicates a deterioration in math skills among girls relative to boys4.
Why does this gap matter? Scoring above the median in eighth grade math increases the likelihood of entering accelerated math paths, allowing students to take AP Statistics & Trigonometry and Calculus. Students who scored below the median in math missed out on these opportunities: 2% took Statistics & Trigonometry and only 1% took Calculus. Overall, boys are more likely to enroll in calculus than girls5.
The gender math gap is also evident in the subgroup of students who took the ACT exam6. ACT scores show that girls do well in reading but underperform boys in math and science, with a wider gap in math (Table 1).
Table 1 - ACT Scores by Subject and Gender
| Gender | Number of test-takers | Avg. Science score | Avg. Math score | Avg. Reading score | Avg. ACT composite score |
|---|---|---|---|---|---|
| Female | 58,284 | 22.44 | 22.56 | 23.21 | 22.78 |
| Male | 47,995 | 23.81 | 24.07 | 23.27 | 23.40 |
| Total in sample who took the ACT* | 106,279 | 23.06 | 23.241 | 23.24 | 22.82 |
| *This figure is lower than the original sample size because ACT scores were not reported for 22% of students. | |||||
These math trends continue in more recent cohorts7 and lend further evidence to the existence of a gender math gap among Minnesota high school graduates.
Just as eighth grade math scores influence high school course-taking patterns, ACT math scores influence the choice of postsecondary major. Table 2 documents gender imbalances by major as well as the relationship between major and average ACT math scores among completers of a Bachelor's degree. The table also displays earnings outcomes six years after high school in the Twin Cities Metro Area.
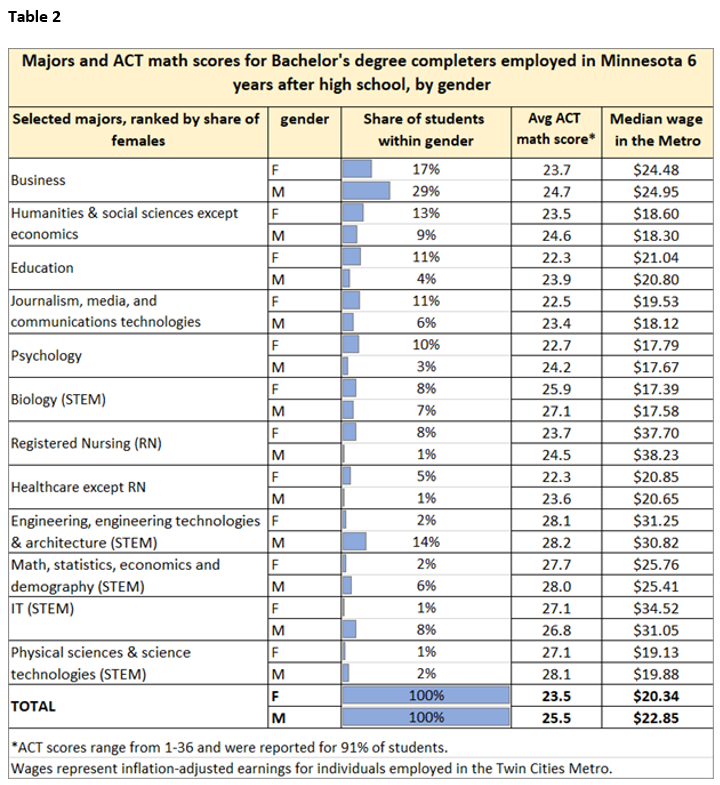
The main takeaways from this analysis are:
This evidence shows that equalizing choice of postsecondary major might be unattainable without first equalizing math proficiency in 11th grade, which in turn stems from math proficiency in 8th grade. Waiting until 12th grade to try to equalize choice of postsecondary major is too late because paths toward career preparation begin to diverge by gender much sooner.
Figure 2 shows that students employed in the Twin Cities Metro who scored at or above the median in 11th grade math, which we label "high-achieving" for simplicity (the solid blue and green lines) had higher earnings six years after high school than low-achieving students. The uptick in wage trajectories in the solid lines four years after graduation marks the point at which high-achieving students typically complete a postsecondary credential and enter better paying jobs than those held by low-achieving students, who are least likely to complete a credential.
Figure 2
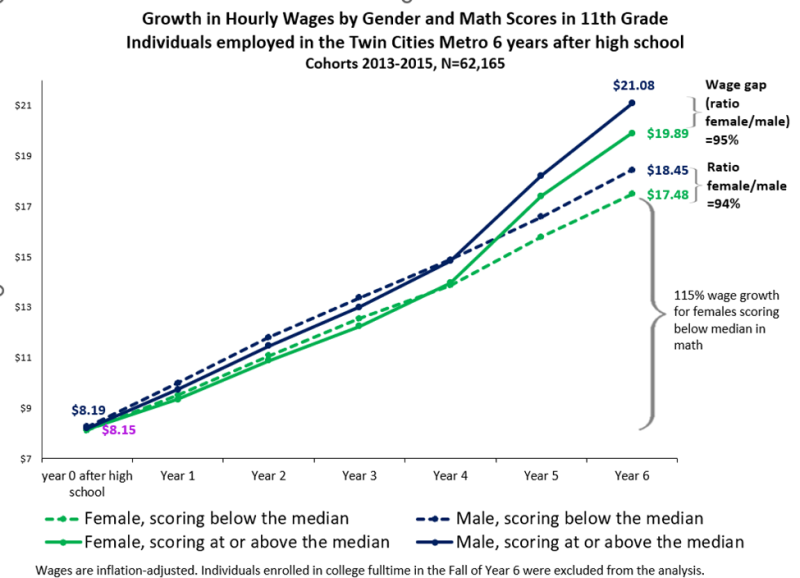
Math achievement had a similar impact on earnings between males and females, as shown by nearly parallel earnings trajectories leading to an almost identical wage gap after 6 years; high-achieving females earned 95% of the wage of their male counterparts while low-achieving females earned 94% of the wage of their male counterparts.
It is tempting to conclude from all of this evidence that math preparedness in 11th grade is critical to students' earnings. However, the math uber alles claim has some limits. It fails to explain, among other things, why males and females with lower-than-median math skills have such different earnings outcomes in Greater Minnesota (Figure 3).
Figure 3
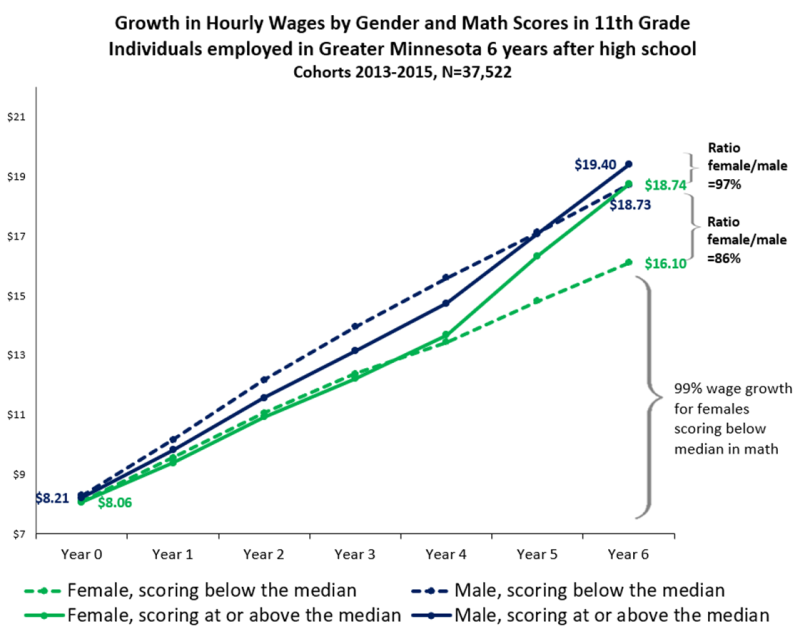
Males scoring below the median (blue dotted line) experienced rapid wage growth immediately after high school and ended up with a large wage advantage over their female peers (green dotted line): $18.74 versus $16.10. This corresponds to a ratio of 86% between the earnings of females and those of males. Given that $18.85 is the family-sustaining wage9, it is clear that the transition from high school to career is far less successful for females with low math achievement. This result is concerning also because low-achieving females represent the majority - 59% - of females in Figure 3.
The high earnings of males with lower-than-median math skills are driven by students who took more than 100 hours of Career & Technical (CTE) courses in the skilled trades10, representing 40% of the group. CTE appears to have given these students marketable skills or work-based experiences that helped them overcome their early math gaps or compensate for them.
Could the gaps illustrated in Figures 2 and 3 stem from differences in what men and women study in high school or in college? Or might they stem from differences in how men and women participate in the labor market after finishing their education? To answer these questions this analysis uses data on some of the most important factors known to influence job productivity and, therefore, earnings. The analysis distinguishes between factors that are fixed such as age or that emerge before entering the labor market (Table 3) and factors that develop through participation in the labor market (Table 4). For reasons of length, the tables display only variables with a statistically significant effect on earnings.
Table 3
| Gender differences in demographics and educational characteristics among individuals employed in Minnesota 6 years after high school graduation, Cohorts 2013-2015, N= 101,120 | |||
|---|---|---|---|
| - | Number | Female | Male |
| Total | 101,120 | 52,973 | 48,147 |
| Percent | - | 52% | 48% |
| Demographics | |||
| White | 79,902 | 52% | 48% |
| Not white | 21,218 | 54% | 46% |
| Eligible for free or reduced-price lunch (1) | 11,812 | 53% | 47% |
| Ever spoken a language different from English at home | 36,572 | 55% | 45% |
| Ever attended an Area Learning Center, Alternative Learning Program, or Vocational Cooperative (2) | 28,800 | 51% | 49% |
| Location of high school and work | |||
| Attended high school in the Twin Cities Metro | 54,829 | 53% | 47% |
| Attended high school in Greater Minnesota | 46,291 | 52% | 48% |
| Employed in the Twin Cities Metro in Year 6 | 63,163 | 53% | 47% |
| Employed in Greater Minnesota in Year 6 | 37,957 | 52% | 49% |
| MCA reading and math proficiency | |||
| Scored at or above the median in 8th grade MCA reading | 45,807 | 56% | 44% |
| Scored at or above the median in 8th grade MCA math | 44,520 | 50% | 50% |
| Scored at or above the median in 11th grade MCA math | 48,847 | 48% | 52% |
| Advanced Placement and other rigorous course-taking in high school | |||
| Took any Advanced Placement (AP) exams | 31,569 | 56% | 45% |
| Took AP Statistics and Trigonometry | 6,655 | 49% | 51% |
| Passed AP calculus exam | 6128 | 43% | 57% |
| Took any early-college courses (CE or PSEO) (3) | 33,580 | 60% | 40% |
| Career & Technical Education (CTE) courses in high school, selected measures | |||
| Took CTE with a work-based learning component (e.g., internships) | 3,524 | 51% | 49% |
| Took any CTE courses related to Construction, Repair (e.g., HVAC), Engineering Technologies, and Precision Production (e.g., welding) | 24,100 | 19% | 81% |
| Took >=150 CTE hours in Business, except non-math related fields (4) | 18,944 | 47% | 53% |
| Took >=150 CTE hours in Fashion, Interior Design (FAID) and Photography | 6495 | 73% | 28% |
| Took >=150 CTE hours in Family and Consumer Sciences (FACS), including Early Childhood Education | 5,735 | 72% | 28% |
| Took >=150 CTE hours in Culinary Arts, Cosmetology, and Hospitality | 4,979 | 79% | 21% |
| Took >=150 CTE hours in Health Care | 3,677 | 79% | 21% |
| Postsecondary outcomes 7 years after high school | |||
| Never enrolled | 10,303 | 37% | 63% |
| Enrolled and left postsecondary school without a credential | 28,492 | 46% | 54% |
| Sub-baccalaureate certificate or Associate's degree | 15,646 | 55% | 45% |
| Bachelor's or above | 44,438 | 59% | 42% |
| Enrolled without completing and still in college | 2,241 | 63% | 37% |
| (1) This is an indicator of socio-economic status.
(2) Alternative Schools are choice-based programs whose mission is to serve students who have not found success in traditional schools. (3) Concurrent Enrollment (CE) and Post-Secondary Enrollment Options (PSEO) allow students to earn college credits while enrolled in courses that are not part of their high school curriculum. (4) Excluded categories are secretarial services, business communications, and hospitality management, which are among the least math-related business subjects. |
|||
While certain characteristics are equally distributed among employed men and women in the dataset, others are not. Percentages of females higher than 52% (the overall share of females in the sample) signal that a certain characteristic was more prevalent among females. The characteristics with the greatest gender imbalance were the following:
These results are further demonstration of how math proficiency, interest in math, or both can shape course choices. While girls don't shy away from taking academically challenging high school coursework such as AP, they were under-represented in the two AP courses focused on math. CTE course-taking patterns also suggest that males were more likely to participate in CTE courses that could have boosted their math skills. A stated goal of CTE is to embed STEM content in the curriculum to give students opportunities to meet math and science credits as an alternative to regular STEM courses, through hands-on learning experiences11. CTE courses in the trades, for example, include STEM content such as blueprint reading, drafting/CAD, trigonometry, computer programming, physics and production technologies. Previous studies12 have shown that manufacturing employers desperately seek candidates with these skills and often recruit directly from high school CTE programs in the skilled trades.
What about factors that emerge after entering the labor market? The biggest gender differences in workplace characteristics are in industry of employment (Table 4). The industries with the closest gender balance are Professional and Technical Services and Firm Headquarters.
Table 4
| Gender differences in selected industry sectors of employment 6 years after high school graduation Cohorts 2013-2015 | |||
|---|---|---|---|
| - | Number | Female | Male |
| Total | 101,120 | 52% | 48% |
| Accommodation and Food Services | 9,314 | 57% | 43% |
| Agriculture, Mining, Utilities | 950 | 22% | 78% |
| Construction | 5,937 | 11% | 89% |
| Education | 6,681 | 72% | 29% |
| Firm Headquarters | 2,948 | 52% | 48% |
| Government | 2,690 | 47% | 53% |
| Hospitals and Clinics | 10,156 | 83% | 17% |
| Manufacturing | 8,149 | 29% | 71% |
| Nursing and Residential Care Facilities | 4,793 | 81% | 19% |
| Retail, Technical Products and Services* | 2,545 | 26% | 74% |
| Retail, All Other | 9,643 | 54% | 46% |
| Professional and Technical Services | 6,789 | 50% | 50% |
| Social Assistance | 4,303 | 82% | 18% |
| Transportation and Warehousing | 2,665 | 25% | 75% |
| Wholesale | 3,678 | 29% | 71% |
| *Representing Automotive/Motor Vehicle Dealers and Building Material Dealers. These retailers have higher skill requirements than other types of retail businesses where females are over-represented. | |||
Mining, Utilities, Construction, Manufacturing, and Wholesale are among the most male-dominated industries in Minnesota. These industries tend to offer union wages, more job stability, and also on-the-job training13.
Our last research question attempts to quantify the association between earnings outcomes and student characteristics in order to identify how much of the gender pay gap still remains after accounting for productivity-related factors, and what part of the gap is attributable to math skills. We use a linear regression technique of the form suggested by Mincer14 to measure the combined effect of all characteristics and identify differences in how each factor contributes to gender pay gaps in the Twin Cities Metro relative to Greater Minnesota. We ran nine regression models for each region using the same variables displayed in Table 3 and 4. Selected results for the Metro regressions are reported in Appendix.
Before interpreting the results, we need to mention that regression is a correlational analysis method and thus does not prove causal effects. In other words, finding that one characteristic is related to an "outcome" variable (e.g., that education level is related to earnings) does not mean that the characteristic is the cause of the outcome.
Figure 4 reports the results from 18 regression models. Each bar represents the effect of being female on earnings, holding other characteristics constant. Therefore each bar represents the gender wage gap, which is always negative because females earn less than males in every model. The length of the bars is measured in logs, which can be interpreted as percentages. The purpose of this analysis is to observe how the effect of being female varies as more information is added to the model, in order to isolate the contribution of each factor net of the characteristics controlled for in the previous steps. Whenever possible, variables were added to the model in chronological order. For example, AP and CTE coursework was added to the model before Concurrent Enrollment and PSEO, because students can take AP and CTE courses from ninth grade while CE and PSEO courses are available almost exclusively in eleventh and twelfth grade.
Figure 4
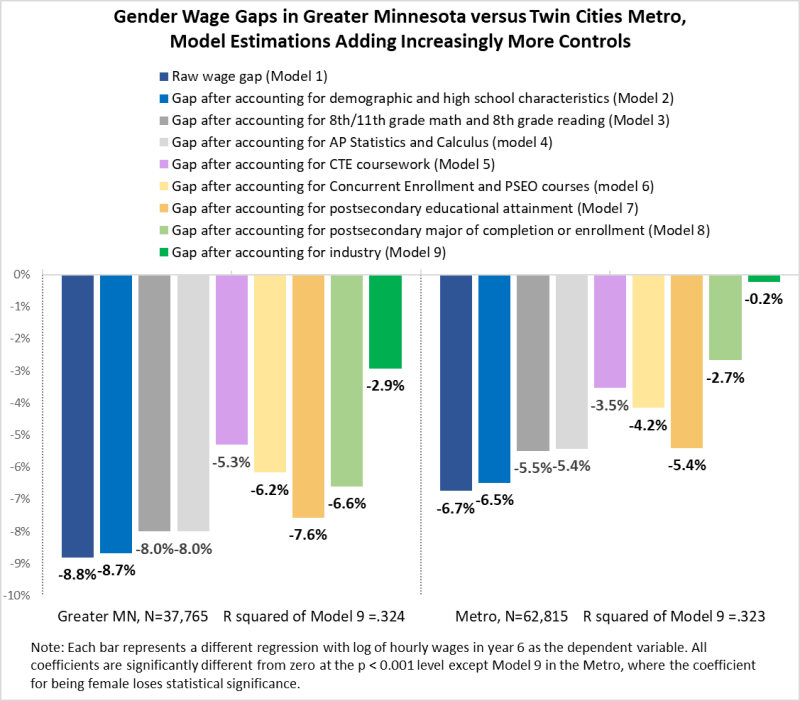
The initial raw gap (Model 1) is higher in Greater Minnesota at -8.8% compared to -6.7% in the Metro. That is, women working in Greater Minnesota were paid around 8.8% less on average than men. Model 2 adjusts the baseline estimate of the wage gap by taking into account the demographics and school characteristics listed on top of Table 3 with a few additional variables15. Accounting for these characteristics leaves the gender gap unchanged (size of the blue bar) because these characteristics are equally distributed across genders.
Model 3 adds controls for math achievement levels (measured in quartiles) in 8th and 11th grade, our metrics of interest. This has the effect of narrowing the gender wage gap in both regions (see dark grey bars), meaning that if females had the same math achievement level as males, gaps would be narrower. This result delivers the proof of an impact of math achievement on the gender wage gap. The effect is larger in the Metro, where the bar shrinks from -6.5% to -5.5% (see regression results in Appendix). This result makes sense because the Metro has a much higher concentration of STEM and STEM-related jobs than the rest of the state. MCA reading levels in 8th and 10th grade were also added to the model. Only 8th grade reading reached statistical significance, but the sign of the coefficient is negative, and its statistical significance disappears when other variables were added to the model (see Appendix). This does not mean that reading skills are not important, but that math scores are a better predictor of future earnings than reading scores.
Model 4 adds variables which control for participation in AP courses. The only AP courses that reach statistical significance are related to math: taking AP Statistics and Trigonometry, taking AP Calculus, and passing the AP Calculus exam16. This again confirms that math knowledge matters to future earnings.
Model 5 adds controls for participation in Career and Technical Education (CTE) courses during high school, including intensity of participation (as concentrators or not), participation in work-based learning such as internships, as well as detailed variables representing 16 fields of study where students took the most hours of CTE instruction. The results (purple bars) provide a big surprise: the gender pay gap decreases starkly. The biggest reduction in the gap is achieved when we add a variable representing whether a student took more than 100 hours of instruction in the skilled trades including Construction, Repair, Engineering/Engineering technologies, and Precision Production.
This result demonstrates two important points. First, CTE course-taking is a meaningful indicator of future career and/or educational choices, which ultimately affect earnings. Second, these choices impact the gender wage gap indicating that CTE gave male students more opportunities to prepare for gainful employment than females. In other words, gender differences in the way students sort into CTE courses favored males regardless of other characteristics controlled for in the model, including math proficiency. This means the most male-dominated CTE pathways boost earnings for students, while the most female-dominated CTE pathways do not. In our models only one female-dominated CTE pathway, healthcare, led to positive effects on earnings.
An additional implication of this result is that male dominance in well-paid jobs not requiring a college degree drives gender wage gaps more than math skills. This dominance begins in high school with boys taking CTE courses in the skilled trades, offering an alternative to college for students with lower-than-median math skills. This explains the results from Figure 3: females are more penalized than males in the Greater Minnesota labor market when their math achievement is low because they are excluded – or steer away from – opportunities for career preparation in the skilled trades.
We could conclude from Model 5 that if CTE course choices were equalized by gender the gender wage gap would be cut by almost half. This goal is immensely difficult to achieve because males' dominance of skilled trades jobs is rooted in social norms and in job requirements often based on physical strength and stamina. A more realistic policy goal would be to mitigate the gender divide in skilled trades CTE.
Model 6 adds controls for early-college courses such as Concurrent Enrollment and PSEO. Adding these variables increases the gender wage gap (see yellow bars) because girls are more likely to participate in these courses in hopes of completing a postsecondary credential faster and with less cost,17 and postsecondary educational attainment has the effect of increasing the gender wage gap.
Model 7 adds controls for postsecondary credential attainment. These variables increase the gender wage gap because females - as shown in Table 3 - hold higher levels of postsecondary education than males. In other words, if males had the same education level as females, wage gaps would be even higher.
Model 8 adds information on postsecondary major of completion or enrollment. Examples of majors with low returns are Psychology, Family and Consumer Sciences (including Early Childhood Education), and Social Work (see regression results in Appendix). In general, college majors and jobs that emphasize service to others are undervalued in labor markets, and they tend to be female-dominated. Choice of major drives earnings for both men and women but has a dramatically different effect on the gender pay gap in the two regions. The female coefficient (light green bar) in the Metro shrinks by a half, from -5.4% to -2.7% (as we expected given the results from Table 3), while the drop in Greater Minnesota is smaller. What seems to be driving gender wage gaps in the Metro is the fact that men disproportionately earn degrees in fields that are well compensated, while in Greater Minnesota it is more common for women to earn less than men even within the same major.
The final model, Model 9, adds information on 26 industry sectors of employment, producing a dramatic reduction in the gap in both regions. The darker green bar in Greater Minnesota shrinks from 6.6% to 2.9%, while in the Metro the gap is entirely wiped out, dropping to 0.2% and losing statistical significance. This means that, holding all other variables constant, gender segregation by industry is responsible for more than half of the gender pay gap in Greater Minnesota and all of the residual gap in the Metro.
The distinction between major and industry is an important one. While major is typically a voluntary choice, industry of employment is the result of job sorting mechanisms in the labor market that individual job seekers have less control over. Finding an association between industry and gender pay gaps, while simultaneously holding major constant, signals that women are less successful than men at entering jobs where their educational investments are fully rewarded. This is a problem of equal opportunities.
Why does the gender pay gap disappear in the Metro but not in Greater Minnesota? This result suggests that some important productivity characteristics related to gender and specific to Greater Minnesota were omitted from the models, or that gender discrimination in the Greater Minnesota labor market is driving up the wage gap. One likely omitted variable is occupation. For example, Construction firms in Greater Minnesota hire relatively more highway maintenance workers and earth drillers than construction firms in the Metro and might hire more males due to the physically strenuous and hazardous nature of these jobs. In contrast, the Metro has more knowledge-economy jobs, which are more gender-neutral and do not give males a productivity advantage.
The result that matters the most to our study is that the variables representing math scores in 8th and 11th grade are statistically significant in all models. This gives strength to the claim that gaps in math skills before and during high school influence post-high school earnings18. The R squared of Model 9 is .324 in Greater Minnesota and .323 in the Metro, meaning that observed characteristics were able to explain 32% (or one-third) of wage variation.
An important caveat to these results is that students' math achievement is also likely associated with characteristics not measured in this study, such as family support of education and other courses taken in high school. Future research should address these limitations by controlling for a broader range of courses taken in high school and by using estimation methods that can correct for omitted variable bias.
This study documents the gender math gap and examines whether it translates into differences in post-high school earnings outcomes between males and females. The main findings are summarized below:
These findings have strong equity implications. Since the transition from high school to career is harder for females, in part because they are less likely to access job skills training in high school and instead wait until postsecondary school, they are more likely to take on a financial burden. Every time a category of workers has to shoulder the cost of skills training more than another category (e.g., females versus males) inequalities will inevitably emerge in the labor market. A category can be defined by gender, race, age, disability, or any other characteristic.
What are the policy implications of these findings? The 9 models depicted in Figure 4 help pinpoint the critical factors that contribute the most to the formation of gender wage gaps. This information can be used to formulate policies to address gender wage gaps at the time in life when these factors emerge. Here is a summary of factors and their policy implications:
Although equalizing math preparedness may seem like a drop in the bucket compared to the daunting systemic forces that produce gender pay gaps, it would improve women's chances to prepare for gainful employment while in high school or completing a credential in financially viable fields. Therefore, it deserves to be part of a workforce equity agenda.
This research uses data on students who graduated from a Minnesota public high school merged with postsecondary student records and Minnesota Unemployment Insurance wage records from the Statewide Longitudinal Education Data System (SLEDS). All students who graduated from high school between 2013 and 2015 are included except GED completers, individuals who graduated after age 20, and students who received special education services in 11th and 12th grade. Finally, since the study's main goal is to measure the role of course-taking behavior on outcomes, we only included students who had a record in each grade (9th, 10th, 11th, and 12th) to avoid bias in the measurement of course-taking patterns.
Appendix: OLS Regressions Controlling for Different Sets of Explanatory Variables
| Dependent Variable: Log of Real Hourly Wages 6 Years After High School Graduation, Twin Cities Metro. N= 62,815 | Model 2: Gender & other demographics | Model 3: 8th/11th grade math | Model 4: Statistics & Calculus | Model 5: CTE courses | Model 6/7: PSEO, CE & PS education level | Model 8: PS Major | Model 9: Industry | |
|---|---|---|---|---|---|---|---|---|
| Gender | Female | -0.0647*** | -0.0550*** | -0.0542*** | -0.0366*** | -0.0536*** | -0.0271*** | -0.0024 |
| MCA score quartiles in 8th/11th grade (reference: first quartiles) | 25th-49th percentile in 8th grade math (second quartile) | - | 0.0162*** | 0.0173*** | 0.01718*** | 0.0126* | 0.0119** | 0.0111** |
| 50th-75th pctile in 8th grade math | - | 0.0216*** | 0.0214*** | 0.0219*** | 0.0130*** | 0.0112* | 0.0118** | |
| >75th pctile in 8th grade math | - | 0.0521*** | 0.0360*** | 0.0375*** | 0.0264*** | 0.0223*** | 0.0238*** | |
| 25-49th pctile in 11th grade math | - | 0.0226*** | 0.0234*** | 0.0238*** | 0.0097*** | 0.0116** | 0.0079* | |
| 50-75th pctile in 11th grade math | - | 0.0491*** | 0.0463*** | 0.0480*** | 0.0196*** | 0.0179*** | 0.0127** | |
| >75th pctile in 11th grade math | - | 0.0960*** | 0.0726*** | 0.0772*** | 0.0394*** | 0.0323*** | 0.0246*** | |
| >=50th pctile (median and above) in 8th grade reading | - | -0.0097** | -0.0124*** | -0.0076* | -0.0157*** | -0.0070* | -0.0038 | |
| AP | Took AP Statistics and Trig. | - | - | 0.0416*** | 0.0436*** | 0.0369*** | 0.0284*** | 0.0243*** |
| Passed AP Calculus exam | - | - | 0.0547*** | 0.0546*** | 0.0572*** | 0.0415*** | 0.0114* | |
| CTE courses | Took CTE with work-based learning | - | - | - | 0.0393*** | 0.0402*** | 0.0391*** | 0.0332*** |
| Took >=100 hours in skilled trades | - | - | - | 0.0556*** | 0.0631*** | 0.0512*** | 0.0301*** | |
| Took >=100 hours in auto-repair | - | - | - | 0.0390*** | 0.0621*** | 0.0503*** | 0.0463*** | |
| Took >=100 hours in healthcare | - | - | - | 0.0491*** | 0.0597*** | 0.0383*** | 0.0314*** | |
| CE & PSEO | Took PSEO courses | - | - | - | - | 0.0627*** | 0.0555*** | 0.0479*** |
| Took Concurrent Enrollment | - | - | - | - | 0.0137*** | 0.0139*** | 0.0120*** | |
| Postsecondary education level (reference: not enrolled) | Enrolled and dropped out within 6 years from high school exit | - | - | - | - | -0.0389*** | -0.0593*** | -0.0219*** |
| completed a credential below Bachelor's | - | - | - | - | 0.0407*** | -0.0208*** | -0.0249*** | |
| Completed a BA or graduate certif. | - | - | - | - | 0.1046*** | 0.0926*** | 0.0687*** | |
| Completed a Master's degree | - | - | - | - | 0.0764*** | 0.0653*** | 0.0719*** | |
| Did not complete and still in school | - | - | - | - | -0.0693*** | -0.0919*** | -0.0534*** | |
| Major of enrollment or completion (reference: not enrolled or no major) | Registered Nursing | - | - | - | - | - | 0.3412*** | 0.3305*** |
| IT | - | - | - | - | - | 0.1550*** | 0.1212*** | |
| Engineering/Engineering technology | - | - | - | - | - | 0.1635*** | 0.1094*** | |
| Family and consumer sciences | - | - | - | - | - | -0.0934*** | -0.0274*** | |
| Journalism, media and communications | - | - | - | - | - | -0.0384*** | -0.0319*** | |
| Psychology | - | - | - | - | - | -0.1293*** | -0.0925*** | |
| Construction | - | - | - | - | - | 0.0547*** | 0.0547*** | |
| Repair and transportation | - | - | - | - | - | 0.1296*** | 0.1296*** | |
| Precision production | - | - | - | - | - | 0.0598*** | 0.0598*** | |
| Industry (reference: retail) | Agriculture, Mining, and Utilities | - | - | - | - | - | - | 0.2818*** |
| Construction | - | - | - | - | - | - | 0.4039*** | |
| Advanced manufacturing | - | - | - | - | - | - | 0.2154*** | |
| Wholesale | - | - | - | - | - | - | 0.2382*** | |
| Nursing and residential care fac. | - | - | - | - | - | - | 0.0351*** | |
| Social assistance | - | - | - | - | - | - | -0.0238*** | |
| - | Fixed effects (cohort, race, disability status, high school characteristics) | Yes | Yes | Yes | Yes | Yes | Yes | Yes |
| - | Adjusted R square | 0.080 | 0.093 | 0.098 | 0.105 | 0.137 | 0.216 | 0.323 |
| ***Coefficients are statistically significant at the p <=0.001 level. ** Statistically significant at the <=0.01 level. *Statistically significant at the <=0.05 level. | ||||||||
1Source: WalletHub 2021.
2Minnesota Comprehensive Assessment (MCA). Given that a new baseline for 8th grade math was set in 2011, we used the median and 75th percentile in each cohort to determine the three categories displayed in Figure 1.
3The categories displayed in Figure 1 were calculated based on quartile distributions of MCA scores in 8th and 11th grade by graduation year cohort included in this study. See "About the data" for detailed information on sample inclusion criteria.
4If, instead of score quartiles, we had used MDE's proficiency categories (does not meet proficiency, meets proficiency, exceeds proficiency) the widening of the math gap between boys and girls in 11th grade would have been even more pronounced.
5 In our dataset, 13% of boys took the AP Calculus exam versus 10% of girls.
6TheACT test is the most widely administered college entrance exam in the U.S.
7See Minnesota SLEDS.
8Although some experts treat all healthcare occupations and corresponding training programs as STEM, this study does not.
9According to the cost of living tool, a family-sustaining wage in Minnesota in 2020 was $18.85. This benchmark is based on the most typical family structure in Minnesota of one fulltime worker, one part-time worker, and one child.
10As documented in this study, males who participated in CTE as concentrators and focused in the trades (Construction, Repair, Precision Production, Engineering/Engineering Technologies) had higher wages compared to other students regardless of differences in postsecondary education level.
11CTE courses may provide an opportunity for 9th-12th grade students to develop a deeper understanding of mathematics and science through hands-on learning. CTE programs are offered in 81% of Minnesota high schools.
12Source: 2019 Minnesota Hiring Difficulties survey, Table 2.
13Students who participated in CTE in the skilled trades – and were overwhelmingly male – were working in these industries the year after high school graduation at significantly higher rates than other students (23% versus 15%) regardless of their 11th grade math achievement. This contributes to the excellent wage outcomes of males with low math achievement in Figure 3.
14See Jacob Mincer, Schooling, Experience, and Earnings, Columbia University Press, 1974.
15Additional variables include race; disability status and disability type; graduation cohort; 8th grade attendance; English Learner status; having graduated from a charter or International Baccalaureate school; having ever attended an online school; Planning Region of schooling and of employment.
16Some students register for the AP calculus exam but obtain a grade lower than 3, which means failing. Gender disparities in Calculus course enrollment improved over time but still persist. In 2021, 51.2% of males took Calculus (while males represented 50.7% of total enrollment) versus 48.8% of females (while females represented 49.2% of total enrollment). Source: Minnesota Department of Education.
17If we could control for CE and PSEO course subjects we would likely see no change, or even a reduction, in the gender wage gap.
18To clarify this result, we added to the model an interaction between gender and a dummy representing whether students scored at or above the median in 11th grade math. The interaction is positive and significant in Greater Minnesota, meaning that the wage gap is smaller when women are proficient in math, and math achievement gives a greater boost to the earnings of females than of males. This is the most complete explanation of gender wage gaps shown in Figure 3: males with low math achievement were able to find well-paying jobs out of high school even controlling for other variables. This suggests that math achievement matters more to the earnings of females in the Greater Minnesota labor market.
19As demonstrated in a previous study, none of the pathways pursued by female CTE concentrators led to family-sustaining wages without a postsecondary credential. See Table 4 in Leibert, Females in Career and Technical Education, MN Economic Trends March 2022.
20Embedding STEM content across its curriculum is already a stated goal of CTE, but historically it has been implemented unevenly across female-dominated and male-dominated course offerings.